R Ionosphere Knit
Description: This is my first Rmd that I fully coded myself. It’s based off of a set of data collected by a radar system in Canada. There are a total of 34 independent variables in the dataset that I used to create this KNN model.
The data and more information about it can be found at data.world by following this link. And the repo can be found on Github here.
suppressMessages(library(tidyverse))
suppressMessages(library(pander))
suppressMessages(library(class))
df <- read.csv("https://query.data.world/s/a7daatpbbqbht722grkkm3ws522yhg?dws=00000",
header = TRUE, stringsAsFactors = FALSE)
# Display the structure of the underlying data
str(df)
## 'data.frame': 350 obs. of 35 variables:
## $ X1 : int 1 1 1 1 1 1 0 1 1 1 ...
## $ X0 : int 0 0 0 0 0 0 0 0 0 0 ...
## $ X0.99539 : num 1 1 1 1 0.0234 ...
## $ X.0.05889 : num -0.18829 -0.03365 -0.45161 -0.02401 -0.00592 ...
## $ X0.85243 : num 0.9304 1 1 0.9414 -0.0992 ...
## $ X0.02306 : num -0.36156 0.00485 1 0.06531 -0.11949 ...
## $ X0.83398 : num -0.10868 1 0.71216 0.92106 -0.00763 ...
## $ X.0.37708 : num -0.936 -0.121 -1 -0.233 -0.118 ...
## $ X1.1 : num 1 0.89 0 0.772 0.147 ...
## $ X0.03760 : num -0.0455 0.012 0 -0.164 0.0664 ...
## $ X0.85243.1: num 0.5087 0.7308 0 0.528 0.0379 ...
## $ X.0.17755 : num -0.6774 0.0535 0 -0.2028 -0.063 ...
## $ X0.59755 : num 0.344 0.854 0 0.564 0 ...
## $ X.0.44945 : num -0.69707 0.00827 0 -0.00712 0 ...
## $ X0.60536 : num -0.5169 0.5459 -1 0.3439 -0.0457 ...
## $ X.0.38223 : num -0.97515 0.00299 0.14516 -0.27457 -0.1554 ...
## $ X0.84356 : num 0.05499 0.83775 0.54094 0.5294 -0.00343 ...
## $ X.0.38542 : num -0.622 -0.136 -0.393 -0.218 -0.102 ...
## $ X0.58212 : num 0.331 0.755 -1 0.451 -0.116 ...
## $ X.0.32192 : num -1 -0.0854 -0.5447 -0.1781 -0.0541 ...
## $ X0.56971 : num -0.1315 0.7089 -0.6997 0.0598 0.0184 ...
## $ X.0.29674 : num -0.453 -0.275 1 -0.3558 0.0367 ...
## $ X0.36946 : num -0.1806 0.4339 0 0.0231 0.0152 ...
## $ X.0.47357 : num -0.35734 -0.12062 0 -0.52879 0.00888 ...
## $ X0.56811 : num -0.2033 0.5753 1 0.0329 0.0351 ...
## $ X.0.51171 : num -0.2657 -0.4022 0.907 -0.6516 -0.0154 ...
## $ X0.41078 : num -0.2047 0.5898 0.5161 0.1329 -0.0324 ...
## $ X.0.46168 : num -0.184 -0.2215 1 -0.5321 0.0922 ...
## $ X0.21266 : num -0.1904 0.431 1 0.0243 -0.0786 ...
## $ X.0.34090 : num -0.11593 -0.17365 -0.20099 -0.62197 0.00732 ...
## $ X0.42267 : num -0.1663 0.6044 0.2568 -0.0571 0 ...
## $ X.0.54487 : num -0.0629 -0.2418 1 -0.5957 0 ...
## $ X0.18641 : num -0.13738 0.56045 -0.32382 -0.04608 -0.00039 ...
## $ X.0.45300 : num -0.0245 -0.3824 1 -0.657 0.1201 ...
## $ g : chr "b" "g" "b" "g" ...
# Display the first six lines
head(df)
## X1 X0 X0.99539 X.0.05889 X0.85243 X0.02306 X0.83398 X.0.37708 X1.1
## 1 1 0 1.00000 -0.18829 0.93035 -0.36156 -0.10868 -0.93597 1.00000
## 2 1 0 1.00000 -0.03365 1.00000 0.00485 1.00000 -0.12062 0.88965
## 3 1 0 1.00000 -0.45161 1.00000 1.00000 0.71216 -1.00000 0.00000
## 4 1 0 1.00000 -0.02401 0.94140 0.06531 0.92106 -0.23255 0.77152
## 5 1 0 0.02337 -0.00592 -0.09924 -0.11949 -0.00763 -0.11824 0.14706
## 6 1 0 0.97588 -0.10602 0.94601 -0.20800 0.92806 -0.28350 0.85996
## X0.03760 X0.85243.1 X.0.17755 X0.59755 X.0.44945 X0.60536 X.0.38223 X0.84356
## 1 -0.04549 0.50874 -0.67743 0.34432 -0.69707 -0.51685 -0.97515 0.05499
## 2 0.01198 0.73082 0.05346 0.85443 0.00827 0.54591 0.00299 0.83775
## 3 0.00000 0.00000 0.00000 0.00000 0.00000 -1.00000 0.14516 0.54094
## 4 -0.16399 0.52798 -0.20275 0.56409 -0.00712 0.34395 -0.27457 0.52940
## 5 0.06637 0.03786 -0.06302 0.00000 0.00000 -0.04572 -0.15540 -0.00343
## 6 -0.27342 0.79766 -0.47929 0.78225 -0.50764 0.74628 -0.61436 0.57945
## X.0.38542 X0.58212 X.0.32192 X0.56971 X.0.29674 X0.36946 X.0.47357 X0.56811
## 1 -0.62237 0.33109 -1.00000 -0.13151 -0.45300 -0.18056 -0.35734 -0.20332
## 2 -0.13644 0.75535 -0.08540 0.70887 -0.27502 0.43385 -0.12062 0.57528
## 3 -0.39330 -1.00000 -0.54467 -0.69975 1.00000 0.00000 0.00000 1.00000
## 4 -0.21780 0.45107 -0.17813 0.05982 -0.35575 0.02309 -0.52879 0.03286
## 5 -0.10196 -0.11575 -0.05414 0.01838 0.03669 0.01519 0.00888 0.03513
## 6 -0.68086 0.37852 -0.73641 0.36324 -0.76562 0.31898 -0.79753 0.22792
## X.0.51171 X0.41078 X.0.46168 X0.21266 X.0.34090 X0.42267 X.0.54487 X0.18641
## 1 -0.26569 -0.20468 -0.18401 -0.19040 -0.11593 -0.16626 -0.06288 -0.13738
## 2 -0.40220 0.58984 -0.22145 0.43100 -0.17365 0.60436 -0.24180 0.56045
## 3 0.90695 0.51613 1.00000 1.00000 -0.20099 0.25682 1.00000 -0.32382
## 4 -0.65158 0.13290 -0.53206 0.02431 -0.62197 -0.05707 -0.59573 -0.04608
## 5 -0.01535 -0.03240 0.09223 -0.07859 0.00732 0.00000 0.00000 -0.00039
## 6 -0.81634 0.13659 -0.82510 0.04606 -0.82395 -0.04262 -0.81318 -0.13832
## X.0.45300 g
## 1 -0.02447 b
## 2 -0.38238 g
## 3 1.00000 b
## 4 -0.65697 g
## 5 0.12011 b
## 6 -0.80975 g
# Display the field headers
names(df)
## [1] "X1" "X0" "X0.99539" "X.0.05889" "X0.85243"
## [6] "X0.02306" "X0.83398" "X.0.37708" "X1.1" "X0.03760"
## [11] "X0.85243.1" "X.0.17755" "X0.59755" "X.0.44945" "X0.60536"
## [16] "X.0.38223" "X0.84356" "X.0.38542" "X0.58212" "X.0.32192"
## [21] "X0.56971" "X.0.29674" "X0.36946" "X.0.47357" "X0.56811"
## [26] "X.0.51171" "X0.41078" "X.0.46168" "X0.21266" "X.0.34090"
## [31] "X0.42267" "X.0.54487" "X0.18641" "X.0.45300" "g"
# Display a summary of various results for each field
summary(df)
## X1 X0 X0.99539 X.0.05889
## Min. :0.0000 Min. :0 Min. :-1.0000 Min. :-1.00000
## 1st Qu.:1.0000 1st Qu.:0 1st Qu.: 0.4715 1st Qu.:-0.06539
## Median :1.0000 Median :0 Median : 0.8708 Median : 0.01670
## Mean :0.8914 Mean :0 Mean : 0.6403 Mean : 0.04467
## 3rd Qu.:1.0000 3rd Qu.:0 3rd Qu.: 1.0000 3rd Qu.: 0.19473
## Max. :1.0000 Max. :0 Max. : 1.0000 Max. : 1.00000
## X0.85243 X0.02306 X0.83398 X.0.37708
## Min. :-1.0000 Min. :-1.00000 Min. :-1.0000 Min. :-1.00000
## 1st Qu.: 0.4126 1st Qu.:-0.02487 1st Qu.: 0.2091 1st Qu.:-0.05348
## Median : 0.8086 Median : 0.02117 Median : 0.7280 Median : 0.01508
## Mean : 0.6003 Mean : 0.11615 Mean : 0.5493 Mean : 0.12078
## 3rd Qu.: 1.0000 3rd Qu.: 0.33532 3rd Qu.: 0.9704 3rd Qu.: 0.45157
## Max. : 1.0000 Max. : 1.00000 Max. : 1.0000 Max. : 1.00000
## X1.1 X0.03760 X0.85243.1 X.0.17755
## Min. :-1.00000 Min. :-1.00000 Min. :-1.00000 Min. :-1.00000
## 1st Qu.: 0.08679 1st Qu.:-0.04900 1st Qu.: 0.01918 1st Qu.:-0.06409
## Median : 0.68243 Median : 0.01755 Median : 0.66770 Median : 0.02975
## Mean : 0.51045 Mean : 0.18176 Mean : 0.47511 Mean : 0.15599
## 3rd Qu.: 0.95056 3rd Qu.: 0.53619 3rd Qu.: 0.95816 3rd Qu.: 0.48361
## Max. : 1.00000 Max. : 1.00000 Max. : 1.00000 Max. : 1.00000
## X0.59755 X.0.44945 X0.60536 X.0.38223
## Min. :-1.0000 Min. :-1.00000 Min. :-1.0000 Min. :-1.00000
## 1st Qu.: 0.0000 1st Qu.:-0.07180 1st Qu.: 0.0000 1st Qu.:-0.07787
## Median : 0.6457 Median : 0.03050 Median : 0.5978 Median : 0.00000
## Mean : 0.4002 Mean : 0.09496 Mean : 0.3434 Mean : 0.07243
## 3rd Qu.: 0.9561 3rd Qu.: 0.37562 3rd Qu.: 0.9195 3rd Qu.: 0.31168
## Max. : 1.0000 Max. : 1.00000 Max. : 1.0000 Max. : 1.00000
## X0.84356 X.0.38542 X0.58212 X.0.32192
## Min. :-1.0000 Min. :-1.000000 Min. :-1.0000 Min. :-1.00000
## 1st Qu.: 0.0000 1st Qu.:-0.222532 1st Qu.: 0.0000 1st Qu.:-0.22580
## Median : 0.5882 Median : 0.000000 Median : 0.5728 Median : 0.00000
## Mean : 0.3806 Mean :-0.002526 Mean : 0.3588 Mean :-0.02317
## 3rd Qu.: 0.9362 3rd Qu.: 0.195467 3rd Qu.: 0.9003 3rd Qu.: 0.13672
## Max. : 1.0000 Max. : 1.000000 Max. : 1.0000 Max. : 1.00000
## X0.56971 X.0.29674 X0.36946 X.0.47357
## Min. :-1.0000 Min. :-1.000000 Min. :-1.0000 Min. :-1.00000
## 1st Qu.: 0.0000 1st Qu.:-0.237063 1st Qu.: 0.0000 1st Qu.:-0.35608
## Median : 0.4982 Median : 0.000000 Median : 0.5321 Median : 0.00000
## Mean : 0.3360 Mean : 0.009167 Mean : 0.3625 Mean :-0.05622
## 3rd Qu.: 0.8968 3rd Qu.: 0.188820 3rd Qu.: 0.9129 3rd Qu.: 0.16490
## Max. : 1.0000 Max. : 1.000000 Max. : 1.0000 Max. : 1.00000
## X0.56811 X.0.51171 X0.41078 X.0.46168
## Min. :-1.0000 Min. :-1.00000 Min. :-1.0000 Min. :-1.00000
## 1st Qu.: 0.0000 1st Qu.:-0.32375 1st Qu.: 0.2836 1st Qu.:-0.42899
## Median : 0.5492 Median :-0.01491 Median : 0.7085 Median :-0.01768
## Mean : 0.3956 Mean :-0.06993 Mean : 0.5420 Mean :-0.06842
## 3rd Qu.: 0.9072 3rd Qu.: 0.15792 3rd Qu.: 1.0000 3rd Qu.: 0.15486
## Max. : 1.0000 Max. : 1.00000 Max. : 1.0000 Max. : 1.00000
## X0.21266 X.0.34090 X0.42267 X.0.54487
## Min. :-1.0000 Min. :-1.00000 Min. :-1.0000 Min. :-1.000000
## 1st Qu.: 0.0000 1st Qu.:-0.23494 1st Qu.: 0.0000 1st Qu.:-0.239347
## Median : 0.4992 Median : 0.00000 Median : 0.4469 Median : 0.000000
## Mean : 0.3789 Mean :-0.02701 Mean : 0.3523 Mean :-0.002248
## 3rd Qu.: 0.8846 3rd Qu.: 0.15422 3rd Qu.: 0.8595 3rd Qu.: 0.200935
## Max. : 1.0000 Max. : 1.00000 Max. : 1.0000 Max. : 1.000000
## X0.18641 X.0.45300 g
## Min. :-1.0000 Min. :-1.00000 Length:350
## 1st Qu.: 0.0000 1st Qu.:-0.16101 Class :character
## Median : 0.4131 Median : 0.00000 Mode :character
## Mean : 0.3498 Mean : 0.01582
## 3rd Qu.: 0.8168 3rd Qu.: 0.17211
## Max. : 1.0000 Max. : 1.00000
# Assigning the values "g" and "b" in field AI to "good" and "bad" respectively
df$g <- factor(df$g, levels = c("g", "b"), labels = c("good", "bad"))
# Creating a method to normalize data between 0 and 1
max_min_normalize <- function(x) {
return((x - min(x)) / (max(x) - min(x)))
}
# Testing the previous function against a first group of numbers
v1 <- c(1, 2, 3, 4, 5)
max_min_normalize(v1)
## [1] 0.00 0.25 0.50 0.75 1.00
# Testing the previous function against a second group of numbers
v2 <- c(10, 20, 30, 40, 50)
max_min_normalize(v2)
## [1] 0.00 0.25 0.50 0.75 1.00
# Removing field B because the data adds no value
df_n <- select(df, -X0)
# Creating a new data frame without field AI and applying the normalization function
df_n2 <- as.data.frame(lapply(df_n[-34], max_min_normalize))
# Checking to see if the normalization is working correctly
summary(df_n2)
## X1 X0.99539 X.0.05889 X0.85243
## Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
## 1st Qu.:1.0000 1st Qu.:0.7358 1st Qu.:0.4673 1st Qu.:0.7063
## Median :1.0000 Median :0.9354 Median :0.5083 Median :0.9043
## Mean :0.8914 Mean :0.8202 Mean :0.5223 Mean :0.8002
## 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:0.5974 3rd Qu.:1.0000
## Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
## X0.02306 X0.83398 X.0.37708 X1.1
## Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
## 1st Qu.:0.4876 1st Qu.:0.6046 1st Qu.:0.4733 1st Qu.:0.5434
## Median :0.5106 Median :0.8640 Median :0.5075 Median :0.8412
## Mean :0.5581 Mean :0.7746 Mean :0.5604 Mean :0.7552
## 3rd Qu.:0.6677 3rd Qu.:0.9852 3rd Qu.:0.7258 3rd Qu.:0.9753
## Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
## X0.03760 X0.85243.1 X.0.17755 X0.59755
## Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
## 1st Qu.:0.4755 1st Qu.:0.5096 1st Qu.:0.4680 1st Qu.:0.5000
## Median :0.5088 Median :0.8338 Median :0.5149 Median :0.8228
## Mean :0.5909 Mean :0.7376 Mean :0.5780 Mean :0.7001
## 3rd Qu.:0.7681 3rd Qu.:0.9791 3rd Qu.:0.7418 3rd Qu.:0.9780
## Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
## X.0.44945 X0.60536 X.0.38223 X0.84356
## Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
## 1st Qu.:0.4641 1st Qu.:0.5000 1st Qu.:0.4611 1st Qu.:0.5000
## Median :0.5152 Median :0.7989 Median :0.5000 Median :0.7941
## Mean :0.5475 Mean :0.6717 Mean :0.5362 Mean :0.6903
## 3rd Qu.:0.6878 3rd Qu.:0.9597 3rd Qu.:0.6558 3rd Qu.:0.9681
## Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
## X.0.38542 X0.58212 X.0.32192 X0.56971
## Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
## 1st Qu.:0.3887 1st Qu.:0.5000 1st Qu.:0.3871 1st Qu.:0.5000
## Median :0.5000 Median :0.7864 Median :0.5000 Median :0.7491
## Mean :0.4987 Mean :0.6794 Mean :0.4884 Mean :0.6680
## 3rd Qu.:0.5977 3rd Qu.:0.9502 3rd Qu.:0.5684 3rd Qu.:0.9484
## Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
## X.0.29674 X0.36946 X.0.47357 X0.56811
## Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
## 1st Qu.:0.3815 1st Qu.:0.5000 1st Qu.:0.3220 1st Qu.:0.5000
## Median :0.5000 Median :0.7661 Median :0.5000 Median :0.7746
## Mean :0.5046 Mean :0.6812 Mean :0.4719 Mean :0.6978
## 3rd Qu.:0.5944 3rd Qu.:0.9565 3rd Qu.:0.5824 3rd Qu.:0.9536
## Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
## X.0.51171 X0.41078 X.0.46168 X0.21266
## Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
## 1st Qu.:0.3381 1st Qu.:0.6418 1st Qu.:0.2855 1st Qu.:0.5000
## Median :0.4925 Median :0.8543 Median :0.4912 Median :0.7496
## Mean :0.4650 Mean :0.7710 Mean :0.4658 Mean :0.6895
## 3rd Qu.:0.5790 3rd Qu.:1.0000 3rd Qu.:0.5774 3rd Qu.:0.9423
## Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
## X.0.34090 X0.42267 X.0.54487 X0.18641
## Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
## 1st Qu.:0.3825 1st Qu.:0.5000 1st Qu.:0.3803 1st Qu.:0.5000
## Median :0.5000 Median :0.7234 Median :0.5000 Median :0.7066
## Mean :0.4865 Mean :0.6762 Mean :0.4989 Mean :0.6749
## 3rd Qu.:0.5771 3rd Qu.:0.9297 3rd Qu.:0.6005 3rd Qu.:0.9084
## Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
## X.0.45300
## Min. :0.0000
## 1st Qu.:0.4195
## Median :0.5000
## Mean :0.5079
## 3rd Qu.:0.5861
## Max. :1.0000
# Assigning field AI from the original data set to the variable g
g <- df[,35]
# Combining the data set with the normalized data back with field AI
dat <- cbind(g, df_n2)
# Setting the size of the training data
train_ratio <- .90
# Finding the number of rows to use for training based on the ratio and size of the data set
train_N <- round(train_ratio * nrow(dat)) +1
# Setting the seed value
set.seed(813)
# Finding the rows that will be used to train the model
train_IDs_dat <- sample(1:nrow(dat), size = train_N, replace = FALSE)
# Creating a set of data that will be used to train the model
train_dat <- dat[train_IDs_dat,]
# Creating a set of data that will be used to test the model. Any row that's not in the train data will be in the test data.
test_dat <- dat[-train_IDs_dat,]
# Creating a function that will let us create a frequency table
frqtab <- function(x,caption) { round(100*prop.table(table(x)),2) }
# Checking the frequency of field g in the dat table
ft_whole <- frqtab(dat$g)
# Checking the frequency of field g in the train data
ft_train <- frqtab(train_dat$g)
# Checking the frequency of field g in the test table
ft_test <- frqtab(test_dat$g)
#Combining the previous three values in to one data set and naming the fields
ftcmp_df <- as.data.frame(cbind(ft_whole, ft_train, ft_test))
colnames(ftcmp_df) <- c("Whole", "Training Set", "Test Set")
#Using the pander package to display the frequency of the g field from all three tables
pander(ftcmp_df, style="rmarkdown", caption = "Comparison of good and bad frequency in %")
| Whole | Training Set | Test Set | |
|---|---|---|---|
| good | 64 | 63.92 | 64.71 |
| bad | 36 | 36.08 | 35.29 |
Table: Comparison of good and bad frequency in %
# Setting the K value equal to the square root of the number of rows plus 1
k0 <- round(sqrt(nrow(dat))) +1
# Displaying the number of k values
k0
## [1] 20
# Using the class package to do KNN classification
knn.k0 <- knn(train = train_dat[,-1], test = test_dat[,-1], cl = train_dat[,1], k=k0)
# Determine the Accuracy of the previous classification
accuracy <- round(100*mean(test_dat$g==knn.k0),digits = 2)
cat('\n', 'The overall accuracy is', accuracy, '%')
##
## The overall accuracy is 79.41 %
df_z <- as.data.frame(lapply(df[-35], scale))
df_z2 <- select(df_z, -X0)
g <- df[, 35]
dat <- cbind(g, df_z2)
train_ratio <- .9
train_N <- round(train_ratio * nrow(dat)) + 1
set.seed(813)
train_ID_dat <- sample(1:nrow(dat), size = train_N, replace = FALSE)
train_dat <- dat[train_ID_dat,]
test_dat <- dat[-train_ID_dat,]
k0 <- round(sqrt(nrow(dat))) + 1
knn.k0 <- knn(train = train_dat[, -1], test = test_dat[,-1], cl=train_dat[,1], k=k0)
accuracy_z <- round(100*mean(test_dat$g==knn.k0),digits=2)
accur_cmp.df <- as.data.frame(cbind(accuracy, accuracy_z))
colnames(accur_cmp.df) <- c("Max-Min Normalization", "Z-Score Normalization")
pander(accur_cmp.df, style="rmarkdown", caption="Comparison of normailzation methods: Kappa Coefficient (in %)")
| Max-Min Normalization | Z-Score Normalization |
|---|---|
| 79.41 | 79.41 |
Table: Comparison of normailzation methods: Kappa Coefficient (in %)
df_n2 <- as.data.frame(lapply(df[-35], max_min_normalize))
type <- df[, 35]
dat <- cbind(type, df_z2)
train_ratio <- 813
Accuracy.list <- 813 #
i <- 1
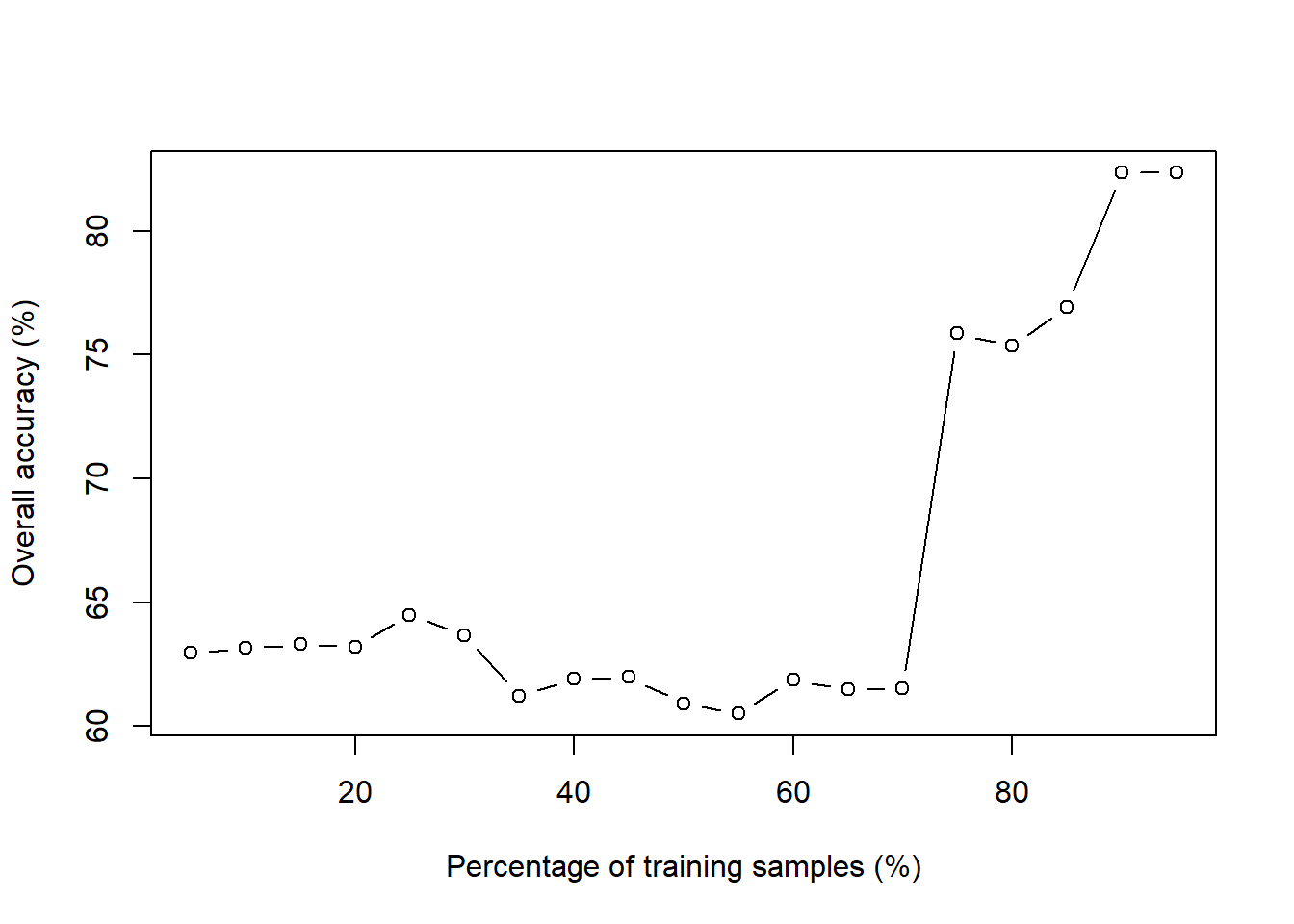
for (train_ratio in seq(from=0.05, to=0.95, by=0.05)){
train_N <- round(train_ratio * nrow(dat)) + 1
set.seed(813)
train_ID_dat <- sample(1:nrow(dat), size = train_N, replace = FALSE)
train_dat <- dat[train_ID_dat, ]
test_dat <- dat[-train_ID_dat, ]
k0 <- round(sqrt(nrow(dat))) + 1
knn.k0 <- knn(train = train_dat[,-1], test = test_dat[,-1], cl=train_dat[, 1], k=k0)
Accuracy.list[i] <- round(100*mean(test_dat$type==knn.k0), digits = 2)
cat('The overall accuracy is ', Accuracy.list[i], '% when the percentage of training samples is', train_ratio*100, '%', '\n') # to print % accuracy
i <- i+1
}
## Warning in knn(train = train_dat[, -1], test = test_dat[, -1], cl = train_dat[,
## : k = 20 exceeds number 19 of patterns
## The overall accuracy is 64.35 % when the percentage of training samples is 5 %
## The overall accuracy is 66.56 % when the percentage of training samples is 10 %
## The overall accuracy is 72.3 % when the percentage of training samples is 15 %
## The overall accuracy is 73.12 % when the percentage of training samples is 20 %
## The overall accuracy is 71.65 % when the percentage of training samples is 25 %
## The overall accuracy is 74.59 % when the percentage of training samples is 30 %
## The overall accuracy is 76.11 % when the percentage of training samples is 35 %
## The overall accuracy is 77.03 % when the percentage of training samples is 40 %
## The overall accuracy is 75.39 % when the percentage of training samples is 45 %
## The overall accuracy is 74.71 % when the percentage of training samples is 50 %
## The overall accuracy is 73.72 % when the percentage of training samples is 55 %
## The overall accuracy is 76.26 % when the percentage of training samples is 60 %
## The overall accuracy is 77.69 % when the percentage of training samples is 65 %
## The overall accuracy is 79.81 % when the percentage of training samples is 70 %
## The overall accuracy is 82.56 % when the percentage of training samples is 75 %
## The overall accuracy is 85.51 % when the percentage of training samples is 80 %
## The overall accuracy is 82.35 % when the percentage of training samples is 85 %
## The overall accuracy is 79.41 % when the percentage of training samples is 90 %
## The overall accuracy is 76.47 % when the percentage of training samples is 95 %
plot(x = seq(from=0.05, to=0.95, by=0.05)*100, y = Accuracy.list, type="b", xlab="Percentage of training samples (%)",ylab="Overall accuracy (%)")
df_n <- as.data.frame(lapply(df[-35], max_min_normalize))
type <- df[, 10]
dat <- cbind(type, df_z2)
train_ratio <- 0.85
train_N <- round(train_ratio * nrow(dat)) + 1
set.seed(813)
train_ID_dat <- sample(1:nrow(dat), size = train_N, replace = FALSE)
train_dat <- dat[train_ID_dat, ]
test_dat <- dat[-train_ID_dat, ]
k_try <- 813
Accuracy.list <- 813
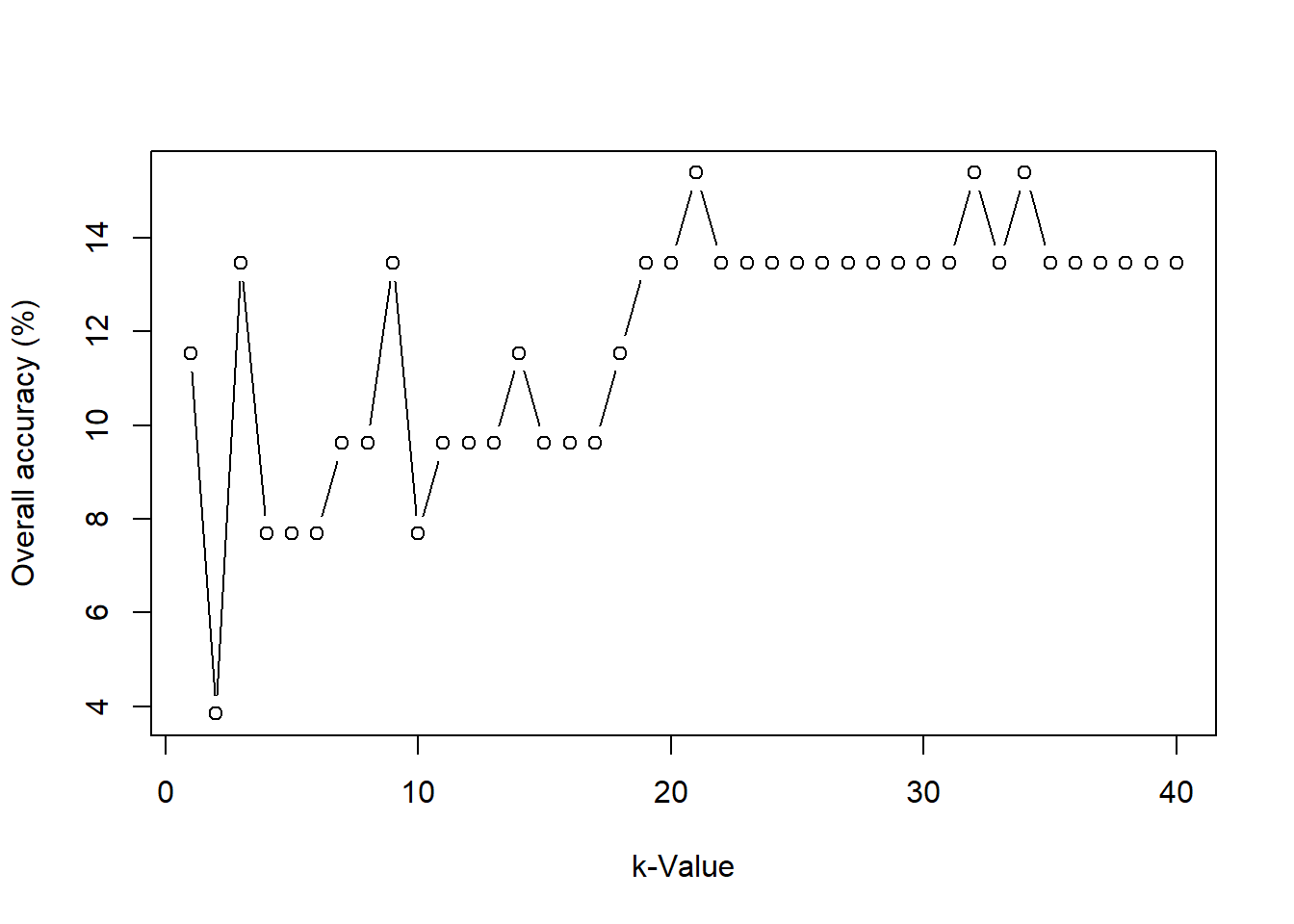
for (k_try in 1 : (k0*2)){
knn.mod <- knn(train = train_dat[,-1], test = test_dat[,-1], cl=train_dat[, 1], k = k_try)
Accuracy.list[k_try] <- round(100*mean(test_dat$type==knn.mod), digits = 2)
cat('When k =', k_try, 'the overall accuracy =', Accuracy.list[k_try], '%\n') # to print % accuracy
}
## When k = 1 the overall accuracy = 7.84 %
## When k = 2 the overall accuracy = 5.88 %
## When k = 3 the overall accuracy = 7.84 %
## When k = 4 the overall accuracy = 5.88 %
## When k = 5 the overall accuracy = 5.88 %
## When k = 6 the overall accuracy = 7.84 %
## When k = 7 the overall accuracy = 5.88 %
## When k = 8 the overall accuracy = 5.88 %
## When k = 9 the overall accuracy = 5.88 %
## When k = 10 the overall accuracy = 5.88 %
## When k = 11 the overall accuracy = 7.84 %
## When k = 12 the overall accuracy = 5.88 %
## When k = 13 the overall accuracy = 5.88 %
## When k = 14 the overall accuracy = 7.84 %
## When k = 15 the overall accuracy = 5.88 %
## When k = 16 the overall accuracy = 5.88 %
## When k = 17 the overall accuracy = 5.88 %
## When k = 18 the overall accuracy = 5.88 %
## When k = 19 the overall accuracy = 5.88 %
## When k = 20 the overall accuracy = 5.88 %
## When k = 21 the overall accuracy = 9.8 %
## When k = 22 the overall accuracy = 7.84 %
## When k = 23 the overall accuracy = 9.8 %
## When k = 24 the overall accuracy = 9.8 %
## When k = 25 the overall accuracy = 9.8 %
## When k = 26 the overall accuracy = 9.8 %
## When k = 27 the overall accuracy = 9.8 %
## When k = 28 the overall accuracy = 9.8 %
## When k = 29 the overall accuracy = 9.8 %
## When k = 30 the overall accuracy = 9.8 %
## When k = 31 the overall accuracy = 9.8 %
## When k = 32 the overall accuracy = 9.8 %
## When k = 33 the overall accuracy = 9.8 %
## When k = 34 the overall accuracy = 11.76 %
## When k = 35 the overall accuracy = 9.8 %
## When k = 36 the overall accuracy = 9.8 %
## When k = 37 the overall accuracy = 9.8 %
## When k = 38 the overall accuracy = 9.8 %
## When k = 39 the overall accuracy = 9.8 %
## When k = 40 the overall accuracy = 9.8 %
plot(x = 1 : (k0*2), y = Accuracy.list, type="b", xlab="k-Value",ylab="Overall accuracy (%)")